Network Pruning with Torch
As my final project for the Computer Vision class thought by Rob Fergus in Fall 2016, I got the project of implementing compression ideas of Song Han presented in paper Learning both Weights and Connections for Efficient Neural Networks. Let’s start with a brief summary of my-work and results.
Get the code at torch-pruner
| No | Section | Work-Done | Result |
|---|---|---|---|
| 1 | Model & Initial Training | I chose Lenet-5 architecture trained on MNIST for my experiments, since it is big enough to compress and small enough to easily do experiments on. | nothing new |
| 2 | Implementing Network Pruning | I start thinking and iterating at how to implement Pruning with Torch. After couple of trial I’ve decided to modify original torch.nn.Linear and torch.nn.SpatialConvolutional modules to mask connections and enable straight-forward training. Torch doesn’t have sparse Tensor implementation and implementing one requires some time. Therefore I decided to focus on the idea and simulate pruning instead of spending too much time on implementing sparse tensors/operations. I prune only weights(biases are untouched) |
|
| 3 | Implementing CUDA version of the script | Realized that it doesn’t make sense not use GPU’s. Implemented -cuda support and enjoyed it. |
2x faster(should be better if I used cudnn instead of cunn) |
| 4 | Layer-wise Sensitivity | Compared the sensity of different layers and effect of retraining/tuning with magnitude based iterative prunning | 3 epoch seemed to be enough for retraining and all-layers have a similar around 10x without-loss compression potential. Retraining of the model provides a significant margin at final compression rate achievable. Different then the paper there is no significant variation between layers in terms of sensitivity. |
| 5 | Iterative Pruning vs One-Shot Pruning | Investigated effect of iterative pruning(pruning a portion of the target rate at each prune/retrain iteration) vs. one-time pruning(pruning the network in one prune/retrain iteration). | An interesting result is even though at some layers(first and last) it provides better results, at intermediate layers iterative prunning doesn’t have a significant superior performance compare to one-shot pruning. |
| 6 | Implementing various Pruning Functions | Attemted to implement five pruner function to investigate different strategies. Completed some | I encountered some problems implementing various pruner functions and decided to go with magnitude based pruning since it gave satisfiying results with our model. |
| 7 | Model-wide Pruning Experiments and Results | Implemented accuracy loss based iterative circular prunning | Interestingly iterative prunning doesn’t cause superior results compare to one-time prunning again as it was in layer-wise pruning experiment. I got my best result with 1-time prunning followed by 20 retraining epoch and got 0.94% error, which is 0.02% improvement in accuracy. The ratio of pruned parameters is 92.9%(which is 14x compression). |
| Next Steps and Conclusion | Plotted weight histograms of best prunning achieved and future work described. | Histograms look promising, similar to the one described in the paper. | |
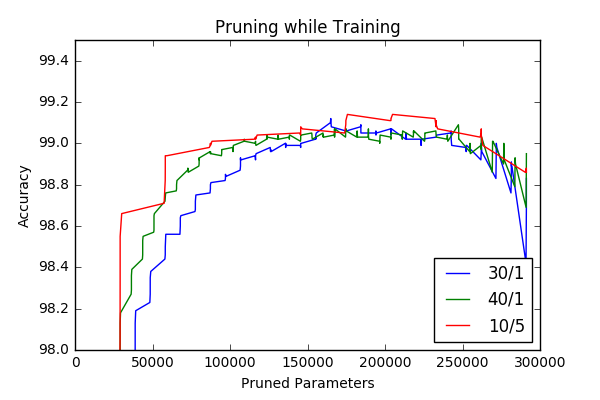
| 9 | Bonus: Last Minute Results | Trained network from zero while prunning | The results are promising, I got 1.05%(-0.09%) accuracy with 40 prunning iterations and 1 retraining epoch after each prunning iteration. |
Model & Initial Training
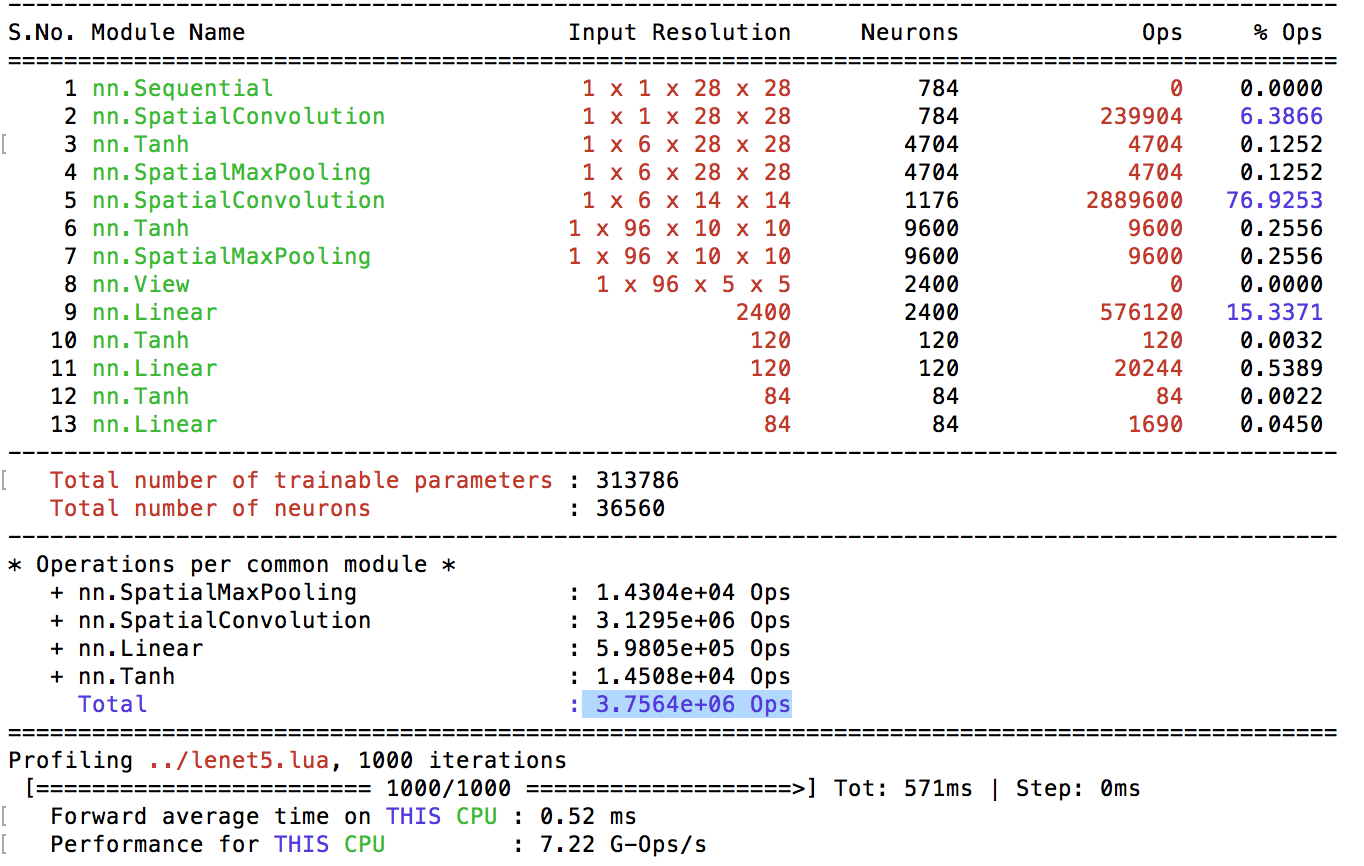
I started with first training my first network LeNet-5 on HPC and got a test error of 0.96% in 30 Epochs with deafult training parameters. It occupies around 5Mb and has 313k parameters. My goal is to get 10x compression in size following the three methods outlined in the paper. The parameter breakdown is below:
Implementing Network Pruning
I wanted to implement every part in Torch. After diving in I realized this might be a hard task. The reason is basically there is no Sparse-Tensor implementation and no space gain is made through making the weigth matrices(connections) sparse. After struggling a bit, I decided to aim an encoding and decoding method. Because implementing Sparse Tensor’s and all the required operations is another project by itself I believe. Layers like SpatialConvolution and Linear is implemented for optimization and source code is not that easy to understand and modify. Therefore I decided to use full weight matrices throughout my experiments and represent connectivity by having non-zero weights.
First I’ve started with Pruner module. After couple of iterations I’ve decided to intialize Pruner module with setVariables call, which includes a model a pruner function(mask generating), a trainer,a tester and relevant torchnet engine. With these parameters I gave full power to the Pruner module to re-train and test model. After initialization one is ready to prune the network. Pruner:pruneLayer call gets a mask-generating function(e.g. Pruner.maskPercentage), layer-id and percentage needed to be pruned. Basically a pruner uses the layer-id’s to get the weight tensor of target layer. Since this is a development code there are no type-checks and the provided id should be a valid one(a layer with .weight field like nn.SpatialConvolution, nn.Linear). Then a mask is generated by calling the provided function with provided parameters and selected weight Tensor. The result is a binary mask with the same size as the weight-Tensor. The mask is saved in each layer and resulting model is tested. After pruning one can call Pruner:reTrain function with nEpochs to retrain the network. Test-accury after testing is returned. More about the functionalites of script, implementation details and a quick-start guide can we found on my github-repo
Implementing CUDA
I didn’t need to implement CUDA for other homeworks, but this time I wanted to learn how to do it and see the difference. I’ve realized that it is pretty straight forward: a generic function isCuda(inp)which calls inp:cuda() if cuda flag is provided does the necessary work. I’ve got a 2x speedup on Lenet-5 model compare to its multithreaded version on NYU’s HPC.
Layer-wise Sensitivity
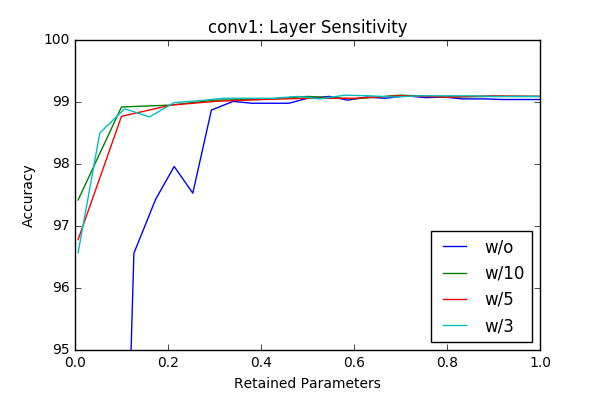
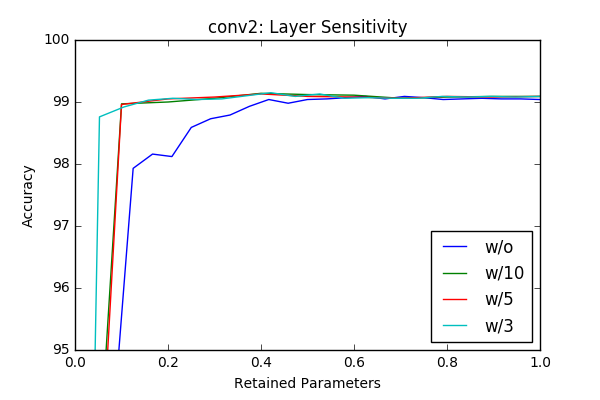
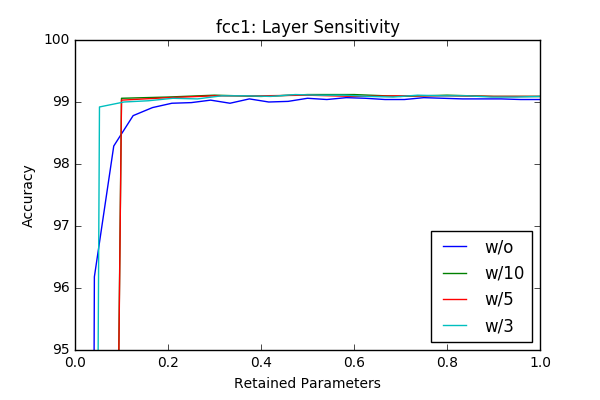
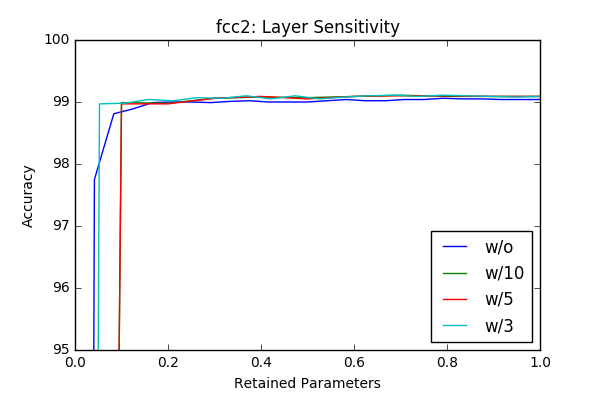
I’ve played with the code and got some initial results by just masking according to the absolute value of the weights and got similar, sometimes better results with around 50% pruning of each layer without retraining. The individual sensitivity of each layer is below. The sensitivities are calculated in an iterative way (More on this is in the next section) by pruning one layer at a time in an iterative way (10-20 iterations).
| conv1-fcc1-fcc3 | conv2-fcc2 |
|---|---|
 |
 |
 |
 |
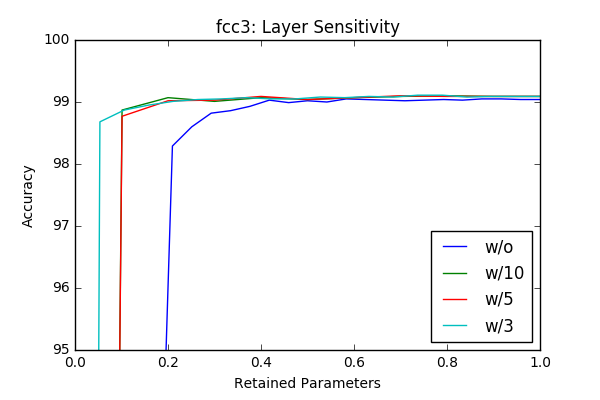 |
w/o flag represents accurcies without reatraining and the others lines represent results with different retraining epochs. For example w/3 is retraining with 3 epochs. Even though the sampling frequency of the graphs make it sometimes hard to compare(I calculated the accurcies for 20 or 10 values of the pruning factor), one can clearly see that retraining of the model provides a significant margin at final compression rate achievable. Another important observation is (different then the paper) there is no significant variation between layers in terms of sensitivity. One last observation is 3 epoch seems enough for retraining the network.
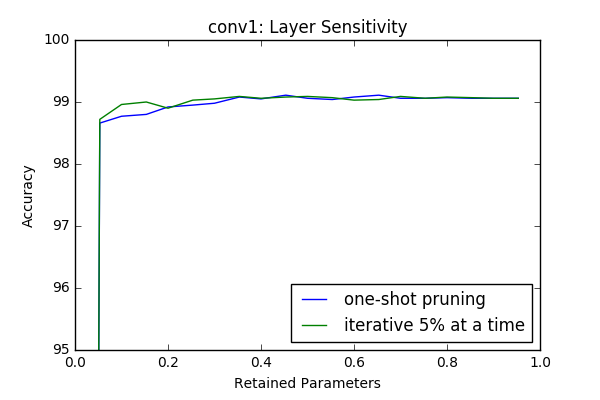
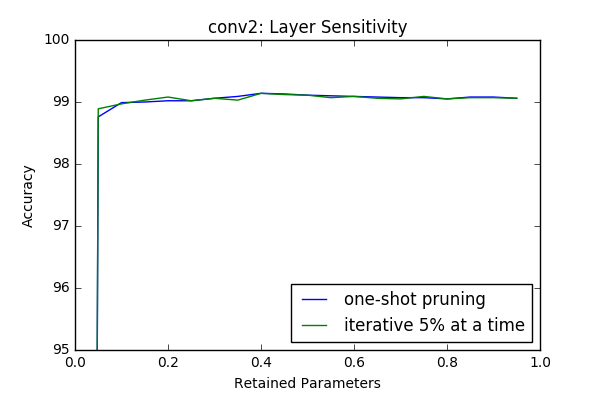
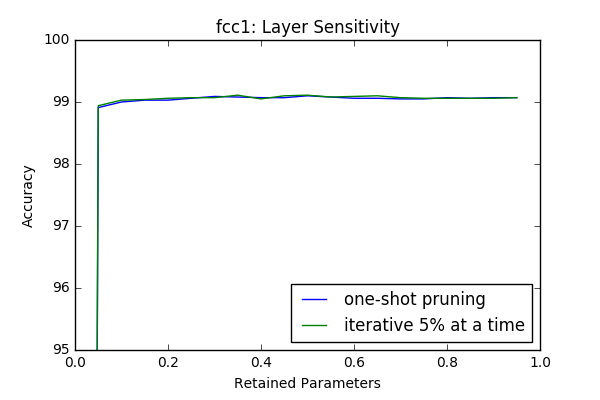
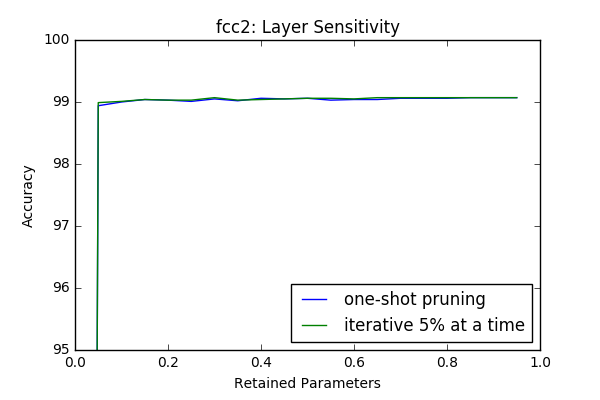
Iterative Pruning vs One-Shot Pruning
In this section I compare iterative pruning with one-shot pruning. In iterative pruning the network or layer is pruned in N steps to its target pruning rate \(c \in [0,1]\), such that at each step \(\frac{c}{N}\) of all parameters are pruned. Whereas in one-shot pruning \(c\) fraction of parametes are pruned immediately. I performed the sensitivity tests(which are done in an iterative manner) in this context again with 3 epoch retraining after each iteration.
| conv1-fcc1-fcc3 | conv2-fcc2 |
|---|---|
 |
 |
 |
 |
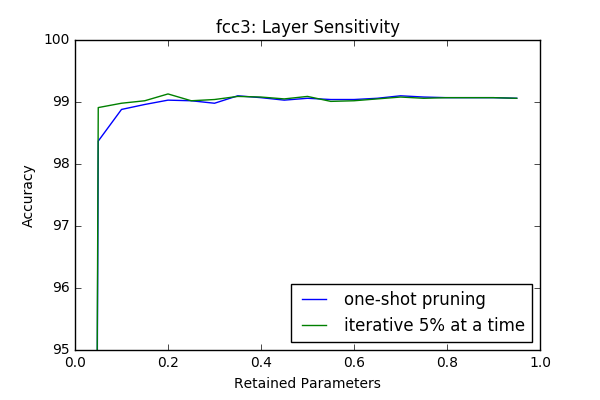 |
An interesting result is even though at some layers(first and last) it provides better results, at intermediate layers iterative prunning doesn’t have a significant superior performance compare to one-shot pruning. However it looks like there is a slight gain if iterative approach used. In the 2-next section I will investigate the effect of one-shot pruning when whole layers are pruned like in a more realistic scenario.
Implementing various Pruning Functions
There are 2 main methods proposed in the literature as pruning metrics.
- Taylor series based approximations of \(\delta E\):
- Using 1st order approximation:
-pruner taylor1 - Using 2nd order diagonal approximation:
-pruner taylor2 - Combining these two
-pruner taylor12
- Using 1st order approximation:
- Regularization based learning methods, where the original weights are multiplied with a constant (initialy 1) and then those constant factors are learned through regularized cost function. Connections with smaller weights are supposed to be less important.
- L1 based
-pruner l1 - L2 based
-pruner l2
- L1 based
- Emprical measure, calculated by pruning each weight one by one and calculating test error for each weight. Then the weights are pruned in the reverse order
-pruner emp
Once start implementing those functionalities, I encountered with some problems. Torch doesn’t have a straight way of implementing L1 and L2. I implemented L2 with weight decay first, however didn’t get superior results to magnitude based pruning. The constant factors were decreasing over training, but it was quite slow and kind of uniform among weights.
Then I tried to implement taylor2, however Torch’s experimental hessian module didn’t worked out. I implemented straight forward taylor1, which is bascially gradWeight*weight and didn’t get good results. At this point I decided to go with magnitude based default pruning.
Later I’ve also implemented emprical scoring of weights, where for each weight I measure the Error of the module when those weight is set to 0. The weights are pruned in decreasing order, since the weights with high Error would also have high \(\delta E=E_{end}-E_{initial}\), since \(E_{initial}\) is same for all weights. Since calculating those scores are a slow process, due to the evaluation on the test set, I’ve performed my experiment on the first convolutional layer conv-1, which has 150 parameters(without biases).
Even though the graph for emprical pruning is sampled with 5 values due to high computation cost it requires, this experiment convinced me that magnitude based pruning works good enough. Therefore I focused on how to prune a network with minimum hyper-parameters, such that one can apply the idea easily to any network.
An important point here to made is, all of the methods above try to approximate or optimize according to the loss function function. However in Optimal Brain Damage paper and during my experiments, I’ve realized that the relationship between loss function and generalization error is not parallel. In other words while trying to pick the less important weights, one doesn’t neceserally get best generalization error.
Model-wide Pruning Experiments and Results
Overall pruning rate is basically set by the layers who has the majority of the parameters. In our model it is the first fully connected layer. Therefore I focused pruning that layer aggresively, whereas I set more lossy rates for other “small” layers. Parameter breakdown and target pruning rates are given.
| Layer | conv1 | conv2 | fcc1 | fcc2 | fcc3 |
|---|---|---|---|---|---|
| Parameters | 150 | 14400 | 288000 | 10080 | 840 |
| Pruning Factors | 0.5 | 0.7 | 0.95 | 0.7 | 0.5 |
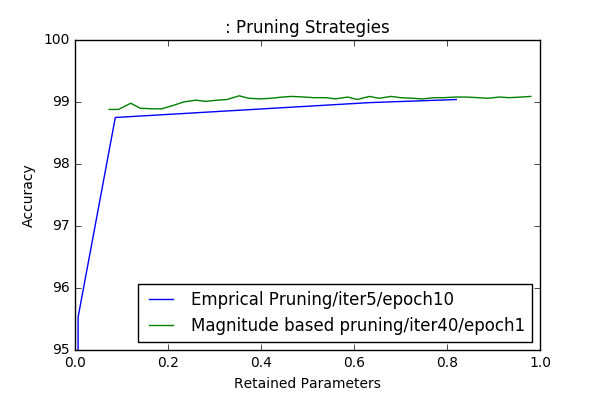
First I did 40 iteration 1 epoch retraining pruning on the network without an accuracy-loss limit. I’ve got 0.99% error, which is 0.03% percent accuracy loss. The ratio of pruned parameters of all model is almost 92.9%. This number doesn’t involve the bias terms, however total number of bias parameters shouldn’t change this ratio significantly. I repeated same strategy for two accuracy-loss limit 0.5% and 1%. However the final result is below these thresholds I got same result as the first one.
As I mentioned I decided to try-out non-iterative prunning strategy and see the effect of iterating pruning in model-scale. In this context I’ve pruned our initial network with different prunning iterations and retraining epochs keeping the layer-wise prunning factors constant. At each prunning iterations a for loop visits all layers and prune a portion of connections and then the model tuned with retraining. For the labels below x/y x represents number of pruning iterations, whereas y represents number of retraining epochs performed after each pruning iteration. To be fair the overall number of retraining epochs during prunning \(x*y\) kept around \(40\) for different experiments. The generalization erros with increasing total number of parameters are plotted below.

Interestingly iterative prunning doesn’t cause superior results compare to one-time prunning again as it was in layer-wise pruning experiment. I go my best result with 1-time prunning followed by 20 retraining epoch and got 0.94%, which is 0.02% better then the first result I got.
Next Steps and Conclusion
Due to the technical work required to implement underlying compressing mechanism, I’ve focused on pruning connections and performed various experiments about the method of pruning. I’ve got even better compression rate then it is given in the original paper. However there are some slight differences between Lenet-5 models I think pruned. I think my initial training was not good as theirs. However I believe my main contribution is:
- A torch implementation of network pruning.
- To show that magnitude-based prunning works actually quite well.
- Layer-wise sensitivity difference doesn’t seem like true.
- Iterative prunning is not significantly better then non iterative one.
I would like to conclude the report with the weight histograms of the pruned network which gave the best result mentioned in the previous section. As can be seen, the parameters follow two gaussian-like clusters as presented in the original paper and I am sure that one can go further and implement weight sharing/quantization and huffman-coding and get overall compression rates around 40x. I am planning to this by implementing it and necessary modules in torch.
Bonus: Last Minute Results
The idea of training an over-paramatized model first and then prunning reported as a ‘natural’ way of learning. However I am not sure this is true. Therefore I’ve trained my model on dataset while pruning some percentage of parameters at each iteration. This is done by starting with a fresh-initiliazed model and performing same prune-retrain iterations. The results are promising, I got 1.05%(-0.09%) percent accuracy with 40 prunning iterations and 1 retraining epoch after each prunning iteration. Results with different iter/epoch combinations result in similar generalization error. I found this really interesting and promising. This process could decrease training and running time if sparse tensors are implemented.